放置玩家几种形式
这是创建地图最后一个教程了,地图做好了,但是有一个很头疼的问题,对那些用河流控制不规则轮廓的地图更是如此,如果是两人地图还好,八人就不一定能生成。我之前给你的地图模板一直使用“rmPlacePlayersCircular(0.35, 0.35, 0.0);//圆形放置玩家”这个语句来放置玩家,但实际上还可以用其他函数放置玩家,下面列出所有放置玩家函数以及解释作用:
[( )] rmPlacePlayer(int playerID, float xFraction, float zFraction): Sets one player location. [( )] rmPlacePlayersCircular(float minFraction, float maxFraction, float angleVariation): Makes a circle of player locations. [( )] rmPlacePlayersLine(float x1, float z1, float x2, float z2, float distVariation, float spacingVariation): Makes a line of player locations. [( )] rmPlacePlayersRiver(int riverID, float distVariation, float spacingVariation, float edgeDistance): Makes a line of player locations along the specified river. [( )] rmPlacePlayersSquare(float dist, float distVariation, float spacingVariationfloat): Makes a square of player locations. [( )] rmSetPlacementTeam(int teamID): Sets the team to place. [( )] rmSetPlacementSection(float fromPercent, float toPercent): Sets the section of the placement line to use ----------------------------------------------------------------------- [( )] rmPlacePlayer(玩家ID, X坐标, Z坐标);//设定某个玩家放置点 [( )] rmPlacePlayersCircular(最小半径, 最大半径, 浮动变化值);//设定圆形放置所有玩家 [( )] rmPlacePlayersLine(X坐标1, Z坐标1, X坐标2, Z坐标2, 浮动变化值, 空间范围大小【数值越大间隔越大】);//直线放置所有玩家 [( )] rmPlacePlayersRiver(int riverID, float distVariation, float spacingVariation, float edgeDistance);所有玩家在某条河流附近放置 [( )] rmPlacePlayersSquare(float dist, 浮动变化值, 空间范围大小);// 方形放置玩家 [( )] rmSetPlacementTeam(int teamID);//将放置所有玩家改成放置某个队伍,0就是队伍1,1就是队伍2。(与int playerID不一样,playerID“0”是大自然,playerID“1”才是玩家1;int teamID“0”是队伍1,teamID“1”是队伍2)**使用该语句后,未设定的队伍将会出局,例如你只设定了队伍1,未设定队伍2会导致所有队伍2的玩家出局。
rmPlacePlayer(1,0.5,0.5); rmPlacePlayer(2,0.3,0.3); rmPlacePlayer(3,0.6,0.6); rmPlacePlayer(4,0.4,0.6); rmPlacePlayer(5,0.1,0.3); |
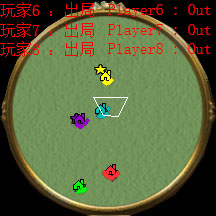 |
rmPlacePlayer(1,0.5,0.5); rmPlacePlayer(2,0.3,0.3); rmPlacePlayer(3,0.6,0.6); rmPlacePlayer(4,0.4,0.6); rmPlacePlayer(5,0.1,0.3); rmPlacePlayer(6,0.5,0.3); rmPlacePlayer(7,0.7,0.5); rmPlacePlayer(8,0.8,0.8); |
 |
rmPlacePlayersCircular(0.35, 0.35, 0.0); |
 |
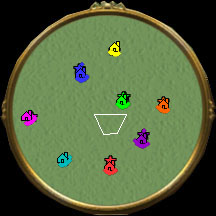
rmPlacePlayersCircular(0.10, 0.45, 0.0); |
 |
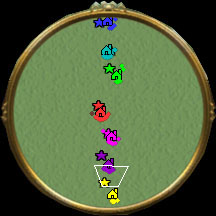
rmPlacePlayersLine(0.0,0.0,1.0,1.0,0,0) |
 |
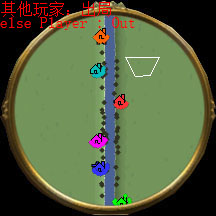
string RiverName ="Northwest Territory Water"; int River2ID = rmRiverCreate(-1, RiverName, 1, 1, 10, 10); rmRiverAddWaypoint(River2ID, 1.0, 1.0 ); rmRiverAddWaypoint(River2ID, 0.0, 0.0 ); rmRiverBuild(River2ID); rmPlacePlayersRiver(River2ID,50,30,20); |
 |
rmSetPlacementTeam(0); rmPlacePlayersLine(0.6,0.9,0.9,0.6,0,50); rmSetPlacementTeam(1); rmPlacePlayersLine(0.6,0.1,0.1,0.6,0,50); |
 |
rmSetPlacementSection(0.6, 0.15); rmPlacePlayersCircular(0.40, 0.40, 0.0); |
 |
rmSetPlacementSection(0.15, 0.60); rmPlacePlayersCircular(0.40, 0.40, 0.0); |
 |
rmSetPlacementSection(0.15, 0.90); rmPlacePlayersCircular(0.40, 0.40, 0.0); |
 |
rmSetPlacementSection(0.9, 0.15); rmPlacePlayersCircular(0.40, 0.40, 0.0); |
 |
rmSetPlacementSection(0.9, 0.5); rmPlacePlayersCircular(0.40, 0.40, 0.0); |
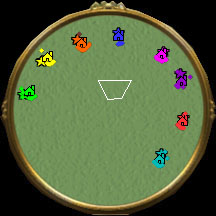 |
rmSetPlacementSection(0.9, 0.6); rmPlacePlayersCircular(0.40, 0.40, 0.0); |
 |
rmSetPlacementSection(0.6, 0.90); rmPlacePlayersCircular(0.40, 0.40, 0.0); |
 |
作者智商不行,无法给出rmSetPlacementSection的用法。我差不多已经是只废喵了 一般的地图都是将团队战(包括1V1)设定为直线放置玩家,两个队伍均在地图的一侧,然后自由就用圆形放置,当然也有直线放置的,对于一些极端的地图,无论用什么语句都不能完整生成八个玩家(有些玩家开局无法生成城镇中心出局),可以采用单个坐标定位例如下面的语句: int FFAType=rmRandInt(rmRandInt(1,2),rmRandInt(3,4)); //定义随机数,用来随机更换玩家位置 //设定8个坐标 float Coordinate1X = 0.76; float Coordinate1Z = 0.835; float Coordinate2X = 0.24; float Coordinate2Z = 0.835; float Coordinate3X = 0.85; float Coordinate3Z = 0.25; float Coordinate4X = 0.15; float Coordinate4Z = 0.25; float Coordinate5X = 0.50; float Coordinate5Z = 0.90; float Coordinate6X = 0.50; float Coordinate6Z = 0.60; float Coordinate7X = 0.65; float Coordinate7Z = 0.15; float Coordinate8X = 0.35; float Coordinate8Z = 0.15; //这个也是坐标,一般是不用设定的,但是为了更改坐标不用一次改四次坐标,所以这样设定 float Player1X = 0.76; float Player1Z = 0.835; float Player2X = 0.24; float Player2Z = 0.835; float Player3X = 0.85; float Player3Z = 0.25; float Player4X = 0.15; float Player4Z = 0.25; float Player5X = 0.50; float Player5Z = 0.90; float Player6X = 0.50; float Player6Z = 0.60; float Player7X = 0.65; float Player7Z = 0.15; float Player8X = 0.35; float Player8Z = 0.15; if(FFAType == 1) /*1234&5678*/ //根据FFAType返回的随机数更换不同的坐标。 { Player1X = Coordinate1X; Player1Z = Coordinate1Z; Player2X = Coordinate2X; Player2Z = Coordinate2Z; Player3X = Coordinate3X; Player3Z = Coordinate3Z; Player4X = Coordinate4X; Player4Z = Coordinate4Z; Player5X = Coordinate5X; Player5Z = Coordinate5Z; Player6X = Coordinate6X; Player6Z = Coordinate6Z; Player7X = Coordinate7X; Player7Z = Coordinate7Z; Player8X = Coordinate8X; Player8Z = Coordinate8Z; } else if(FFAType == 2) /*3412&7856*/ { Player1X = Coordinate3X; Player1Z = Coordinate3Z; Player2X = Coordinate4X; Player2Z = Coordinate4Z; Player3X = Coordinate1X; Player3Z = Coordinate1Z; Player4X = Coordinate2X; Player4Z = Coordinate2Z; Player5X = Coordinate7X; Player5Z = Coordinate7Z; Player6X = Coordinate8X; Player6Z = Coordinate8Z; Player7X = Coordinate5X; Player7Z = Coordinate5Z; Player8X = Coordinate6X; Player8Z = Coordinate6Z; } else if(FFAType == 3) /*2143&6587*/ { Player1X = Coordinate2X; Player1Z = Coordinate2Z; Player2X = Coordinate1X; Player2Z = Coordinate1Z; Player3X = Coordinate4X; Player3Z = Coordinate4Z; Player4X = Coordinate3X; Player4Z = Coordinate3Z; Player5X = Coordinate6X; Player5Z = Coordinate6Z; Player6X = Coordinate5X; Player6Z = Coordinate5Z; Player7X = Coordinate8X; Player7Z = Coordinate8Z; Player8X = Coordinate7X; Player8Z = Coordinate7Z; } else /*4321&8765*/ { Player1X = Coordinate4X; Player1Z = Coordinate4Z; Player2X = Coordinate3X; Player2Z = Coordinate3Z; Player3X = Coordinate2X; Player3Z = Coordinate2Z; Player4X = Coordinate1X; Player4Z = Coordinate1Z; Player5X = Coordinate8X; Player5Z = Coordinate8Z; Player6X = Coordinate7X; Player6Z = Coordinate7Z; Player7X = Coordinate6X; Player7Z = Coordinate6Z; Player8X = Coordinate5X; Player8Z = Coordinate5Z; } //设定8个玩家的定位点 rmSetPlacementTeam(0); rmPlacePlayer(1,Player1X,Player1Z); rmSetPlacementTeam(1); rmPlacePlayer(2,Player2X,Player2Z); rmSetPlacementTeam(2); rmPlacePlayer(3,Player3X,Player3Z); rmSetPlacementTeam(3); rmPlacePlayer(4,Player4X,Player4Z); rmSetPlacementTeam(4); rmPlacePlayer(5,Player5X,Player5Z); rmSetPlacementTeam(5); rmPlacePlayer(6,Player6X,Player6Z); rmSetPlacementTeam(6); rmPlacePlayer(7,Player7X,Player7Z); rmSetPlacementTeam(7); rmPlacePlayer(8,Player8X,Player8Z); 如何判断是否是自由对战呢? 用rmGetIsFFA(): Returns true if this map is set to be a FFA game which means each player on their own team. 例如: if(rmGetIsFFA()==true) { //如果本场游戏是自由对战: } if(rmGetIsFFA()!=true) { //如果本场游戏不是自由对战: } 其他类似语句还有判断是否为王者山丘模式: rmGetIsKOTH(): Returns true if this map is set to be a King of the Hill game. 开局是否为游牧时代:[( )] rmGetNomadStart(): Returns true if this map is to place a covered wagon instead of a town center. 本教程结束。
rmSetPlacementSection(fromPercent,toPercent)坐标计算器
注:为了去除随机性,默认将rmPlacePlayersCircular的min与max相等,浮动设0。
(坐标的)文字设定:
rmSetPlacementSection设定:
地图设定:
rmSetPlacementSection用法已在上面通过多次测试以及推导公式,以下内容仅作保留,其结果自行验证,不保证准确。从方法推理的角度来说来说的确是错了。为什么要保留,哪怕是错了,也是一种探索精神,因为每一次错误的尝试都是向正确答案迈进的一步。
今天翻《圣典》学习“13-4 放置玩家”这一节,关于rmSetPlacementSection用法我有一个猜想,它的两个参数,第一个是开始点位,第二个是结束点位,点位有点像钟表,从0.0-1.2正好转一圈,试了以下感觉基本符合预期。
今天翻《圣典》学习“13-4 放置玩家”这一节,关于rmSetPlacementSection用法我...
rmSetPlacementSection用法
以下文档由孙百里测试、原创:
rmSetPlacementSection和rmPlacePlayersCircular一起结合使用,用来决定玩家的起始位置。rmPlacePlayersCircular代表将所有玩家沿着一段圆弧摆放,其后面所接的数字代表以地图中心为圆心,圆弧所在的圆的半径。rmSetPlacementSection后面所接的两个参数,则分别代表圆弧在该圆上的起点和终点与地图左上-右下对角线所构成的夹角,也就是摆放的第1个玩家和最后一个玩家的位置与地图左上-右下对角线的夹角。
例一:

例二:

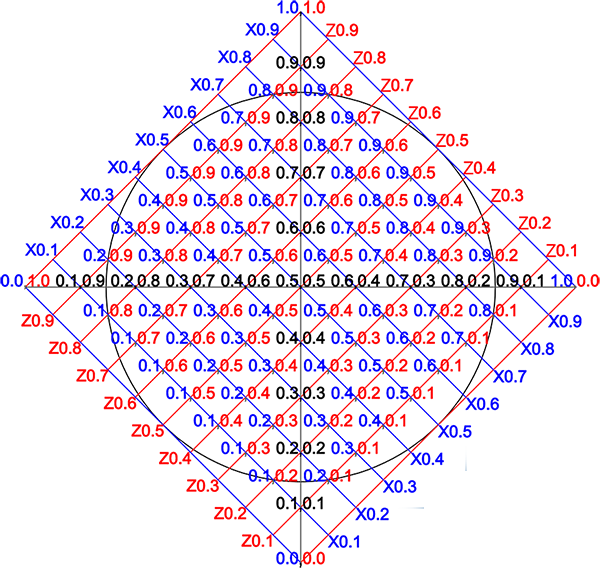 。
。